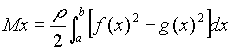
CENTRO DE MASA DE UNA LAMINA PLANA
El centro de masa de una lámina plana es el punto donde el balanceo de la lámina está en equilibrio. El calcular este centro implica el calcular primero su momento (medida de la tendencia de un sistema a girar alrededor de un punto, comúnmente llamado origen) y su masa, en donde aplicaremos la integral definida.
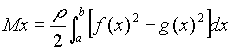
![]()
![]()
Sean g<=f funciones continuas en [a,b]. Para una lámina plana, de densidad uniforme r, delimitada por y , x = a, x = b, los momentos respecto a los ejes x, y son dados :

La masa m de la lámina se obtiene:

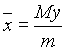
![]()
![]() Y el centro de masa por:
Y el centro de masa por:
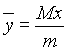
Un ejemplo de esta aplicación de la integral es:
 Para hallar
el centro de masa de la lámina de densidad uniforme r delimitada
por y = 4 - x2 y el eje x, tenemos que:
Para hallar
el centro de masa de la lámina de densidad uniforme r delimitada
por y = 4 - x2 y el eje x, tenemos que:
![]()
Como el centro de masas tiene que estar en el eje de simetría deducimos que
Integrando para calcular su masa obtenemos

El momento con respecto al eje x es:


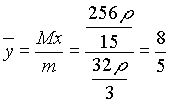 Finalmente:
Finalmente:
El centro de masas es (0, 8/5).